夹江外国语实验学校 王孟宇
【摘要】
植树问题是“数学广角”单元,教材设置了在线段上植树的三种模型,以及在闭合的封闭曲线上植树的问题,通常我们重点在给学生讲授不同的植树方式棵树与间隔数的关系,往往却忽视了植树问题中所渗透的数学思想方法。
【关键词】
植树问题 数形结合 一一对应 思考 解决问题 探索
每次在植树问题的实际教学中,我们总是在很困惑,植树问题该教什么,实际教学时往往毫无头绪,植树问题在现实生活中和实际教学中都应用得非常的广泛。植树问题一年级到五年级都有涉及和涵盖,比如一年级的“之间”,“从……到……”“……之后”,二年级“从第一棵树到第五棵树,一共有多少米?”敲钟问题,爬楼问题等等。那植树问题我们在实际教学中到底该教什么?该让学生学会什么?我认为先要交给学生学会思考的方法,如何来思考?面对不同情景类型的植树问题,最简单和根本的方法就是去画图——数形结合。
通过画图可以把抽象的文字叙述转化成直观而有简单的图形,又通过图形可以把文字信息结合起来,学生更容易理解,信息呈现也更直观,通过图再去分析和思考,抽象的植树问题就会变得更加的简单和直观。在陈雪佳老师的《植树问题》展评课中,充分的运用了数形结合的思想,放手给学生,让学生自己去画图,创作和思考。让学生从最简单直观的图形入手,把抽象的问题变得更直观,更容易去掌握到问题的本质,学生的思维也更加的开阔,会出现思维的碰撞,出现火花,进而才会出现后面的思考和讨论.利用原有的知识储备,去考虑在情景当中出现的问题,去多角度的思考和发现问题.既可以让学生主动去思考,学会思考,又可以培养学生发现问题提出问题的力。
数形结合也是理解题意的好方法,在陈老师的这堂课上,给定的情境是比较复杂的,学生通过画图可以把复杂的情境简单化。
(题目:在通往圆形凉亭的小路一侧植树,小路全长60米,平均分给3个组,每组植20米 ,每隔5米植一棵树,先由第一组从头开始植,植完20米;第二组接着第一组植,第三组再接着第二组植,一直到凉亭,每组各植树多少棵?)
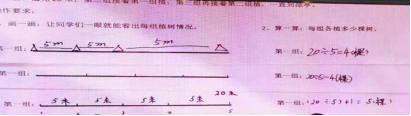
学生通过画图, 第一组该如何来栽树,产生认知冲突引发讨论,让学生渴望去解决。再通过把3个同学创作的作品放在一起来展示,去寻求这些不同作品中的共同点,从而去发现了“间隔数”再去理解路长与间隔数的关系,得到“路长÷间隔长=间隔数”的公式,使知识自然而然的生成,学生经历知识的形成过程由被动变成主动,顺理成章。得到了间隔数,再去思考如何种树的问题,第一小组该如何来种树?3个同学有自己不同的见解,有人认为头不栽,有人认为尾不栽,有人认为头和尾都该栽,引发思考,再回顾题目要求,确定“两端都栽”。
那两端都栽,头要栽,尾也要栽,为什么是20÷5+1却不是+2呢? 再次产生认知冲突,制造矛盾,让学生去质疑和解决,为什么只用+1?学生马上想到了“一一对应”的数学思想,画图。已经有图在了,那就通过连线,“一一对应”把间隔和树对应起来,一棵树对应一个间隔,发现少了一个间隔,只用+1就可以了,从而发现了间隔数和棵树之间的关系。同理可以解决第二组、第三组的植树问题。


陈老师用一个例题,解决了在线段上植树的三种问题,设计非常巧妙的解决了我们以往常常在纠结的这三种模型怎么处理的问题,也让学生在数形结合的思想上自己就探索解决了,改变了以往为了建模而建模的公式化教学。如果在植树问题这堂课中只是建模,让学生生硬的去记住“间隔数+1,间隔数-1,间隔数=棵树”这样的规则,学生永远只是拿着公式去生搬硬套,没有自己的理解和感悟,而且“+1”“-1”这样符号化的东西,太过生硬,学生是非常容易忘记的,忘了怎么办呢?那就是借助图形,通过数形结合,帮助学生去构建知识,让学生对知识有自己的理解和认知。能够自己去发现规律并且运用规律,而不是一个生硬的符号或者数字。
有了数形结合的只是构建,学生对植树问题的理解就很深刻,当陈老师询问学生:“生活中有哪些植树问题?”的时候,学生说得头头是道,比如,学生说到“安装路灯,路灯就相当于树,灯和灯之间的距离就是间隔距离”从学生的发言当中可以看出学生对于植树问题体会非常深刻,有自己的领悟和见解。课堂再升华到,那我们就不仅可以解决线段上的植树问题,还能解决其他的植树问题,比如:弯的,像在凉亭的一圈摆上花盆;在正方形花坛一周种花;方阵的植树问题等等,学生有自己去探索的渴求,也有自己去思考和解决的能力,这就是植树问题这堂课我们该教给学生的,渗透方法并引发思考,让学生自己去思考和探索。
植树问题虽然内容繁多,类型广泛,但是通过数形结合思想的渗透,学生发现了规律,就能按照规律去思考。通过直观且形象的方法,把抽象的文字符号形象具体化,既能够去思考,发现规律,最终利用规律解决问题,这样植树问题就不再是冷冰冰的数字和符号,植树问题不再是公式化的记忆,+1还是-1又有什么重要呢?让植树问题成为数形结合的思想,让它成为存在于学生思考探索问题的一种方法和思考方式。
